テクニカル指標解説:移動平均とは?
ここではテクニカル指標として用いられる「移動平均」について詳しく解説します.
移動平均とは
移動平均にはいくつか種類がありますが,ここではよく用いられる「単純移動平均」と「加重移動平均」と「指数移動平均」を解説します.
単純移動平均とは
単純移動平均はSimple Moving Average(SMA)と呼ばれるもので,式も単純です.
単純移動平均の定義は次の通りです.
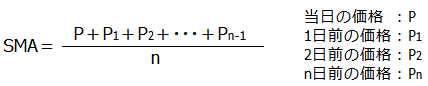
例えば現在のUSD/JPYが10日間で以下のような値動きをしたとします.
|
この場合,単純移動平均は
(82+80+82+79+81+83+82+80+82+81)÷10=81.2 と計算できます.
加重移動平均とは
単純移動平均は計算は単純ですが,直近の価格も昔の価格も同等に評価するため,最近の傾向をうまく反映できない場合があります.
「加重移動平均」は昔の価格も評価するものの最近の価格の方をより高く評価することで最近の傾向を反映しやすくした移動平均です.
※加重移動平均の「現在」と「過去」の評価の度合いを図で表すと次のようになります.
加重移動平均(Weighted Moving Average; WMA) の定義は次の通りです.
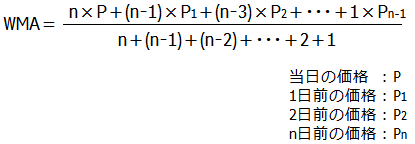
例えば現在のUSD/JPYが10日間で以下のような値動きをしたとします.
|
この場合,加重移動平均は (10×82+9×80+8×82+7×79+6×81+5×83+4×82+3×80+2×82+1×81)÷(10+9+8+7+6+5+4+3+2+1)≒81.15 と計算できます.
この計算からも,直近の値を9日前の価格よりも10倍高く評価していることが分かります.
指数移動平均とは
加重移動平均では直近の価格から昔にさかのぼるにしたがって直線的に評価の割合を減少させましたが,指数移動平均(Exponential Moving Average; EMA) ではその名の通り,指数関数的に評価の割合を減らします.「指数平滑移動平均」とも呼ばれます.
指数移動平均は加重移動平均よりも「さらに最近の価格を重視する」ことができます.
※指数移動平均の「現在」と「過去」の評価の度合いを図で表すと次のようになります.
指数移動平均に使う「減少の度合い(平滑係数)」は次のように定義されます.
αを用いて指数移動平均を式で表すと次の通りです.
当日の終値をPとして,
例えばn=10日とすると,α=0.18となります.
するとEMAtodayは「Pの18%」と「EMAyesterdayの82%」を評価することになります.以下同じようにEMAを順次計算してゆきます.
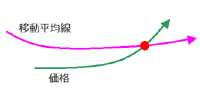
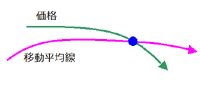
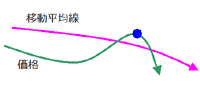
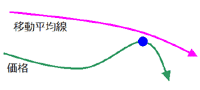
移動平均とグランビルの法則
売買のタイミングをつかむ方法として「グランビルの法則」というものがあります.
これは「移動平均線」と「実際の価格の動き」の2本を用いて買い・売りのタイミングを見極める方法で,「買い」「売り」にそれぞれ4つのタイミングがあります.
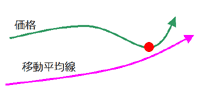
【買いの場合】
|
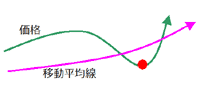
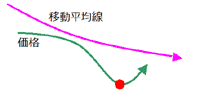
【売りの場合】
|
 | 生活情報アーカイブス TOP |